ポートフォリオのリスク計算|FP1級Wiki
ポートフォリオとは書類ケースを意味します。金融用語ではさまざまな金融商品の組み合わせのことで、細かくまとめたものを言います。おおまかに資産配分することはアセットアロケーションと言います。FP試験ではポートフォリオを組むための計算が計算問題として頻出します。期待収益率、標準偏差。頭が痛くなりますができるだけわかりやすく頑張ります。
期待収益率(期待リターン)
当然ポートフォリオを組むなら将来の収益を予想したい。
そのためにはまず、組み合わせる金融商品ひとつひとつの将来の期待収益率が必要になります。
金融商品の期待収益率の導き方
期待収益率を算出するには、まずこれまでの投資収益率を計算する。
投資収益率(%)=(インカムゲイン+キャピタルゲイン)÷投資金額×100
この投資収益率を1年あたりで計算したものが利回りとなるが、当然これは過去の実績である。
将来のリターンを確率的に予測するには、予想収益率のすべて(この投資商品でこの先起こる可能性を数値化したと言ってもいいかもしれない)について、その確率をウェイトとし、加重平均値を求めることが必要になる。
この加重平均値を「期待収益率(期待リターン)」という。
具体的には、将来の市場の状況を確率的に予測。その市場の状況ごとの投資収益率も予測。それらを加重平均することになる。
FPの試験勉強としてはこの程度に思っていればOKと思います。下記は例題です。
Aさんが証券Aを所有している場合の期待収益率を考えてみます。証券Aはこの先以下のような動きが予測できたとします。
| 生起確率 | 予想収益率 | |
|---|---|---|
| 好況になる | 30% | 10% |
| 普通 | 50% | 5% |
| 不況になる | 20% | ▲5% |
この証券Aの期待収益率はどのようになるかというと、
期待収益率=10%×0.3+5%×0.5+▲5%×0.2=4.5%
証券Aの期待収益率は4.5%と考えることができます。
ポートフォリオの期待収益率
ひとつひとつの期待収益率が出し方がわかった後は、いよいよポートフォリオの期待収益率の出し方です。
今度は個別証券の期待収益率を、自身のポートフォリオの投資比率で加重平均する訳です。
Aさんの所有している証券が先ほどの証券Aだけではなく、不況時のリスクヘッジのために、不況に強い証券Bを所有していたとします。
証券AとBを7:3の割合で所有していた場合のポートフォリオの期待収益率を考えてみます。
| 生起確率 | 証券Aの予想収益率 | 証券Bの予想収益率 | |
|---|---|---|---|
| 好況になる | 30% | 10% | ▲5% |
| 普通 | 50% | 5% | 3% |
| 不況になる | 20% | ▲5% | 7% |
求め方は二通りあります。
期待収益率=(10%×0.7+▲5%×0.3)×0.3+(5%×0.7+3%×0.3)×0.5+(▲5%×0.7+7%×0.3)×0.2=3.57%
あるいは、
- 証券Aの期待収益率=10%×0.3+5%×0.5+▲5%×0.2=4.5%
- 証券Bの期待収益率=▲5%×0.3+3%×0.5+7%×0.2=1.4%
- 加重平均する=4.5%×0.7+1.4%×0.3=3.57%
このようにそれぞれの期待収益率を出した後にそれを加重平均しても求めることができます。
アセットアロケーション
投資目標に合わせて運用資産の配分比率を決めるプロセスのこと。許容するリスクや期待収益率を勘案し、反対の値動きをするものや国内海外などの分散投資も取り入れつつ機動的に行う。どの商品をどのようにいくら買うかまでではなく、大きく資産(アセット)配分(アロケーション)を決定すること。細かい商品の指定はポートフォリオの役割となる。
ポートフォリオのリスク(分散と標準偏差)
分散と標準偏差。もうこうなってくるとただの数学。低学歴の私はもう習ってこなかった部分になります。最後まで苦戦した部分です。ただ、勉強することで意味はわかりました。分散と標準偏差は確かに投資の未来を予想するには必要なんですよ。意味を理解して覚えることで、ただ公式を覚えるよりも身につくのではないかと思います。
証券投資においてのリスクとは投資リターンのばらつき、上下のブレのこと。先ほどまでの期待収益率ではあくまでも確率から平均値をズバリ出したもの。平均ど真ん中をズバー!!ったときの収益率な訳です。ただ、実際にはそんな平均まっしぐらなんて現実に起こるハズがありません。これまで散々学んできた通り、投資運用にはさまざまなリスクが潜んでいるからです(プラスもマイナスもね)。そのリスクによって生じる上下のブレやリターンのばらつき、その度合いを測る尺度として分散と標準偏差が必要となってくるのです!!
分散とはひとつずつ予想収益率から期待収益率を差し引き、その差の2乗の値に生起確率を乗じて、それらを合計した数値のこと。
標準偏差はその分散の平方根のこと。
計算式は言葉で書いても難解過ぎて表現できません。さきほどのAさんの証券Aで説明しましょう。
- 証券Aの期待収益率は4.5%です。
| 生起確率 | 予想収益率 | |
|---|---|---|
| 好況になる | 30% | 10% |
| 普通 | 50% | 5% |
| 不況になる | 20% | ▲5% |
この場合の分散と標準偏差はこうなります。
分散=(10%-4.5%)²×0.3+(5%-4.5%)²×0.5+(▲5%-4.5%)²×0.2=27.25
標準偏差=√27.25=5.22%
ここまでの計算はとにかく基礎編応用編ともに頻出です。覚えてください!!
正規分布
将来のリターンのばらつき度合いは正規分布に従うという考え方を前提にすると、将来発生する収益率の範囲を確率的に把握することができる。
この場合の将来のリターン(収益率)は次のようになる。
- 約68%の確率で期待収益率±1標準偏差の範囲内に収まる
- 約95%の確率で期待収益率±2標準偏差の範囲内に収まる
これ、意味わかります?全然わかんないですよね。頑張って説明します。
まず、正規分布とはこれのことです。
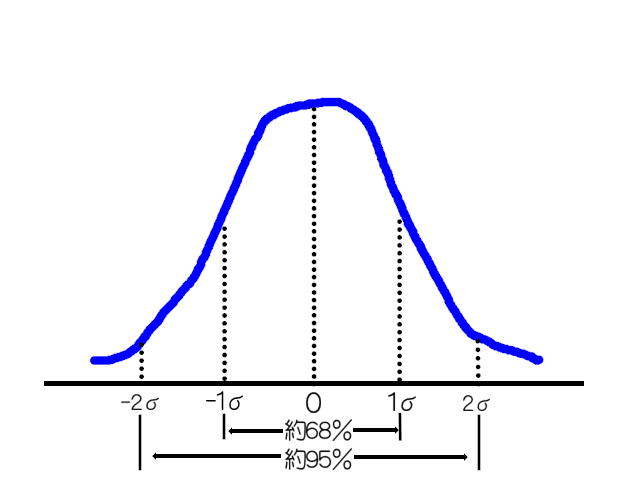
この正規分布は確率分布の最もポピュラーなものだそうです。左右対称で、平均値と最頻値と中央値が一致するという考え方です。
これを基に考えると、68%の確率で±1標準偏差内に収まるし、95%の確率で±2標準偏差内に収まることになります。
これを実際に証券Aで考えてみます。期待収益率4.5%で、標準偏差が5.22%でしたね。
0地点
ゼロ地点はそのまま期待収益率となりますので4.5%。表を見る限りでは4.5%の収益で終わる可能性が一番高いわけですね。
±1標準偏差の範囲
±1標準偏差とは期待収益率を中心にして、標準偏差を前後に1つ分の範囲という意味です。68%がこの収益の範囲に収まると予想できます。
- +1標準偏差=4.5%+5.22%=9.72%
- ー1標準偏差=4.5%ー5.22%=▲0.72%
68%の確率で9.72%~▲0.72%の収益率に収まります。
±2標準偏差の範囲
±2標準偏差とは期待収益率を中心にして、標準偏差を前後に2つ分の範囲という意味です。95%がこの収益の範囲に収まると予想できます。
- +2標準偏差=4.5%+(5.22%×2)=14.94%
- ー2標準偏差=4.5%ー(5.22%×2)=▲5.94%
95%の確率で14.94%~▲5.94%の収益率に収まります。
一般的に、期待収益率と標準偏差がわかれば、ほぼほぼ±2標準偏差が将来のリスクとして考えることができる。
(おまけ)実績収益率から求める標準偏差
証券Aは期待収益率から求める標準偏差でしたが、実績から求める方法もあります。たまに出題されますので覚えておきましょう。
| (出題例) | 第一期 | 第二期 | 第三期 | 第四期 |
| 実績収益率 | 10.00% | 16.00% | ▲20.00% | 10.00% |
①サンプルの平均値を出す。
(10%+16%+▲20%+10%)÷4=4
②サンプルと平均値の差を求め、それぞれ二乗する。
(10-4)²+(16-4)²+(▲20-4)²+(10-4)²=792
*二乗すると負の数もすべて正の数になり平均がデフォルメされます。
③出た答えをサンプル個数で割ります。これが分散となります。
792÷4=198
④分散に平方根を掛ければ標準偏差が出ます。
√198=14.0712=14.07(小数点第3位四捨五入)
ポートフォリオのリスクに関する過去問チャレンジはありません。
外部リンク:金融庁
タグ:ポートフォリオのリスク計算